3x3x3 and 4x4x4 Snake Cube Puzzle

Problem Description

The snake cube puzzle consists of $n^3$ wooden blocks (for $n=3$ forming a 3x3x3 cube) connected by an elastic string threaded through the center of each block. The blocks can rotate relative to each other, allowing the snake to take on various configurations. Besides the ends, each block can be identified as a straight piece or corner piece depending on the angle between the adjacent blocks.

Goal: Find all non-symmetric arrangements of blocks that form a perfect $n^3$ cube.

Mathematical Formulation

The solution can be modeled as finding a Hamiltonian path through an $n^3$ grid graph, where:

• Each block occupies one unit cube position
• Each unit cube position is connected to all adjacent positions that are 1 unit away from it
• The input string defines orientation of each snake block w.r.t. it's neighbors

Let $G = (V, E)$ be the grid graph where:

• $V = \{(x, y, z) : 0 \leq x, y, z \leq n-1\}$ ($n^3$ vertices)
• $E$ represents valid moves between adjacent unit cubes

The path must satisfy: $P = (v_1, v_2, \ldots, v_{n^2})$

where $v_i \in V$ and $(v_i, v_{i+1}) \in E$ for all $i \in \{1, 2, \ldots, n^2-1\}$.

Constraint Analysis

String Orientation Constraints

Each block has a string passing through it with an orientation that determines valid turns:

• Straight blocks: String enters and exits on opposite faces (no turn required)
• Corner blocks: String enters one face and exits on an adjacent face (90° turn)

The sequence of straight and corner blocks defines the constraint signature of the puzzle. Below is an image where the red 3x3x3 puzzle has each of its blocks labeled with either 'S' for straight, or 'C' for corner.

A keen observer may notice that the first and last blocks do not meet either definition, as the string only exits the block from a single face. These blocks are labeled 'S' by defualt, but 'C' would be fine as well. This is addressed in the backtracking algorithm.

Backtracking Algorithm

The backtracking algorithm implements a constrained depth-first-search through the positions of an NxNxN unit cube. The input constraints string must be a perfect cube to represent a valid instance of the puzzle. For instance, a string of length 27 represents a 3x3x3 puzzle while a string of length 64 represents a 4x4x4 puzzle.

Algorithm details

Throughout the depth-first-search from the input starting path, record both $(1)$ a stack of the positions visited and $(2)$ a 3D grid denoting visited positions. The same position cannot be visited twice within the same solution. Use the grid to validate that a position is not yet in the stack in O(1) runtime. Update the 3D grid when visiting each position, then update the 3D grid again to unvisited each position when backtracking. Similarly, maintain a stack of the positions that are visited. Pop the last position from the stack when backtracking. When the depth of the search successfully places the number of cubes in the puzzle, make a copy of the stack and continue backtracking.

Backtracking summary

• Base case: The depth of the search matches the number of cubes in the puzzle, copy the solution path
• Visit neighbors: Identify all valid neighboring positions, and visit them. Valid neighboring positions are within the NxNxN cube, are not occupied, and can be visited subject to the previous block's constraint type.

Sample Solution

The following images include the python solution output and a progression of the solution configuration for the red 3x3x3 puzzle. The red puzzle has the constraint sequence "SSCCCCCCSCCSCCCCCSCCSCCCCSS" pictured above. There are five more symmetric solutions to the one presented here. Some other variants of this puzzle (like the orange one in the background) have more than just one unique asymmetric solution.

Solution Configuration - python script output

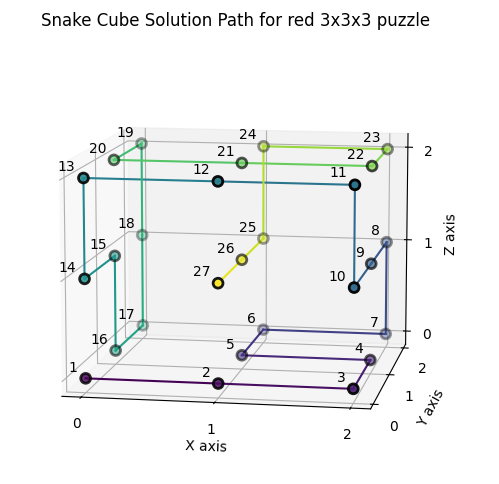
Solution Configuration - process

The first 9 blocks are positioned according to the solution configuration.

The next 9 block are positions according to the solution configuration.

Complete Assembly

The final view shows the fully assembled cube, demonstrating how all blocks fit together perfectly:

This configuration represents one of the valid Hamiltonian paths through the 3×3×3 grid that satisfies all the constraint conditions defined by the snake's physical structure.

Python Implementation

Download the complete Python source code: snake_cube_solver.txt

class SnakeCubeSolver:
    def __init__(self, constraints: str = '',
                 path: List[tuple[int, int, int]] = None,
                 early_stop: bool = True):
        """ Initialize the snake cube solver. """
        ... initialization implementation

    ... additional functions here

    def solve(self, 
              depth: int,
              position: Tuple[int, int, int],
              prev_direction: Tuple[int, int, int] = None) -> bool:
        """
        Recursive backtracking solver for snake cube puzzle using depth-first search.
        Limits search based on constraints representing the shape of the snake.

        Args:
            depth: Current depth in the recursion (block number)
            position: Current position in the cube
            prev_direction: Direction of the previous move

        Returns:
            True if a solution is found, False otherwise
            
        Class Attributes Used:
            self.directions_map: Dict mapping (constraint_type, prev_direction) to
                                 list of precomputed valid directions
            self.constraints: String of 'S' and 'C' defining the instance of the puzzle
            self.cube: 3D list representing the cube state, with 0 for unoccupied
                       and block numbers for occupied
            self.path: Current path of positions taken, list of (x, y, z) tuples
            self.solutions: List to store all found solutions
            self.size: Size of one edge of the cube
            self.size_cubed: Total number of blocks in the cube (size^3)
            self.early_stop: Boolean flag to stop after finding the first solution
        """
        # Base case: all blocks placed
        if depth == self.size_cubed:
            self.solutions.append(self.path[:])
            return True
        
        # Try each direction
        for dx, dy, dz in self.directions_map[self.constraints[depth - 1], prev_direction]:
            
            # Calculate next position
            x, y, z = position[0] + dx, position[1] + dy, position[2] + dz
            
            # Check if next position is inside the bounds and unoccupied
            if not (0 <= x < self.size and 0 <= y < self.size and 0 <= z < self.size) or \
                self.cube[x][y][z] > 0:
                continue
            
            # Mark the cube position and append to path
            self.cube[x][y][z] = depth
            self.path.append((x, y, z))

            # Recursively try this direction
            self.solve(depth + 1, (x, y, z), (dx, dy, dz))
            if self.early_stop and self.solutions:
                return True
            
            # Backtrack the occupied position and path
            self.cube[x][y][z] = 0
            self.path.pop()

        return len(self.solutions) > 0

# Example usage for red puzzle
if __name__ == "__main__":
    path = [(0, 0, 0), (1, 0, 0), (2, 0, 0), (2, 1, 0)]
    solver = SnakeCubeSolver(constraints='SSCCCCCCSCCSCCCCCSCCSCCCCSS',
                            path=path)
    depth = len(path)
    if solver.solve(depth=depth,
                    position=path[-1],
                    prev_direction=solver.calculate_previous_direction(depth=depth)):
        print("Solution found!")
        solver.display_solutions_grid()
    else:
        print("No solution exists.")
# Displays:
"""
Solution found!
Total solutions found: 1
Solution 1:
  1  14  13
 16  15  20
 17  18  19

  2  27  12
  5  26  21
  6  25  24

  3  10  11
  4   9  22
  7   8  23
"""

Complexity Analysis

Time Complexity

Let

• $k$ be the total number of blocks

• $n$ be the cubed root of $k$

• Worst case: $O(5^k)$ or equivalently $O(5^{(n^3)})$

Without considering the constraints that prune the number of neighbors significantly, each position after the starting position could have up to five neighbors. That is, one neighbor to visit for each face excluding the face shared with the previous block in the path.

Therefore, the worst-case time complexity is $O(5^k)$ as we potentially try up to 5 directions at each step. However, with constraint pruning the actual search space is significantly reduced.

Here are some examples of pruning:

• Straight vs corner blocks: Straight blocks have a maximum of 1 valid neighbor, while corner blocks a maximum of 4 valid neighbors

• Constrained to $(0 <= d_i < n)$ for each dimension $d_i$ in $(x,y,z)$: The calculated average count of neighbors is $4.0$ for $n=3$ and $4.5$ for $n=4$. The total number of edges in an NxNxN cube of grid points with unit spacing and edges at shared unit cube faces is $n^2 * (n-1) * 3$.

  • 1. Each slice exposes $n^2$ unit cube faces

  • 2. There are $(n-1)$ slices per axis

  • 3. There are $3$ axes to slice

    The average count of neighbors for each block is twice the number of edges divided by the total number of blocks: $2 * (n^2 * (n-1) * 3) / n^3$.

• Cannot visit the same cell twice: The available neighbors to visit generally decreases as the length of the path increases.

• User specified starting paths: Reduce $k$ by a constant for the number of blocks that can be placed such that symmetric solutions are ignored. In the case of many puzzles, this number was 4.

Space Complexity

• Space: $O(n^3)$ for the recursion stack and path storage
• Grid: $O(n^3)$ for the 3D cube representation
• Solutions: $O(n^3)$ for the list of paths. This assumes that the number of solutions is constant for a given cube. There were about 80 solutions for the orange puzzle before pruning for symmetry, and 10 after pruning.

Optimization Techniques

1. Constraint Propagation: Use the string orientation constraints to immediately prune invalid directions
2. Symmetry Breaking: Start from a fixed path to eliminate symmetric solutions

Attempted techniques

1. Slice checking: Maintain a sum of visited blocks within each slice, invalidating paths that would make a full solution impossible because unvisited blocks are disconnected from each other. This approach was found to be less efficient with the attempted implementation.

Visualization

Results from the python script are presented below in the form of images or GIFs. There are GIFs provided for puzzles that have multiple asymmetric solutions (blue and orange).

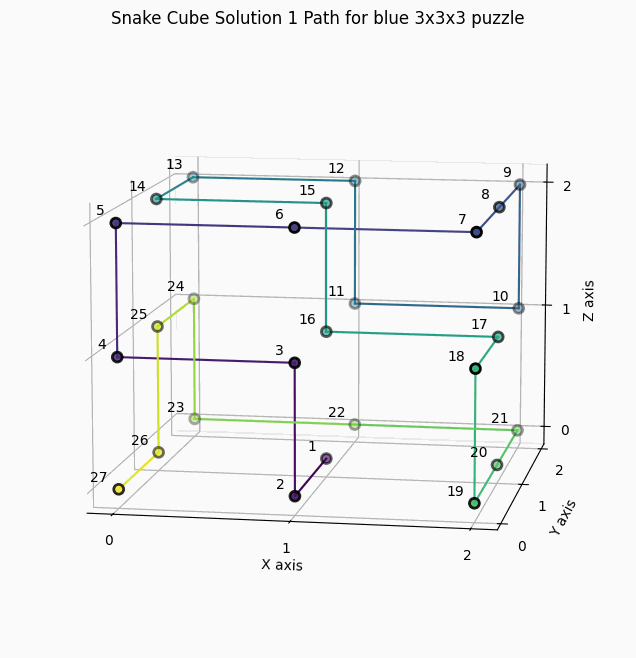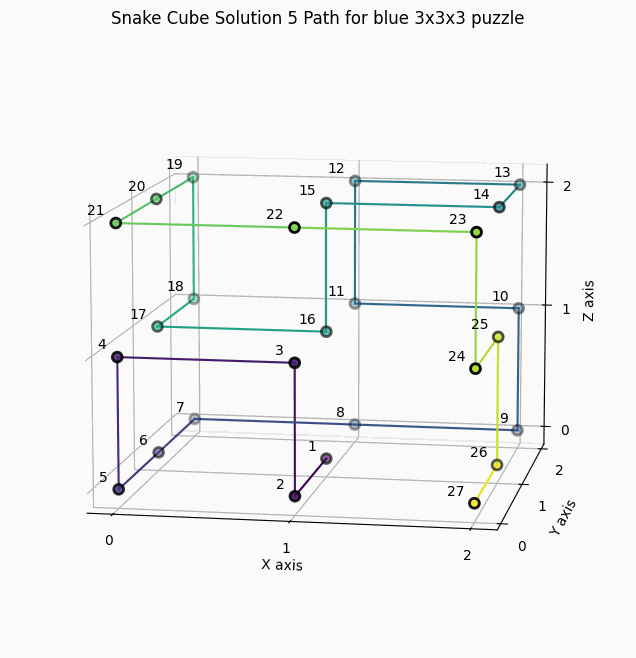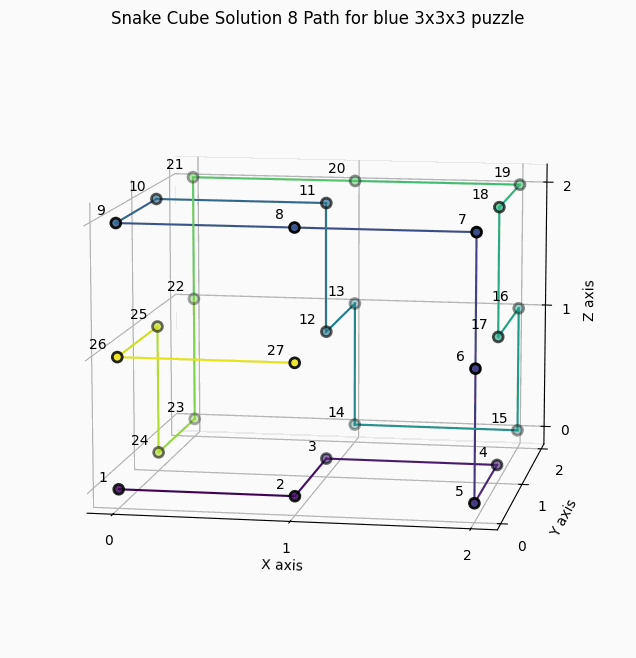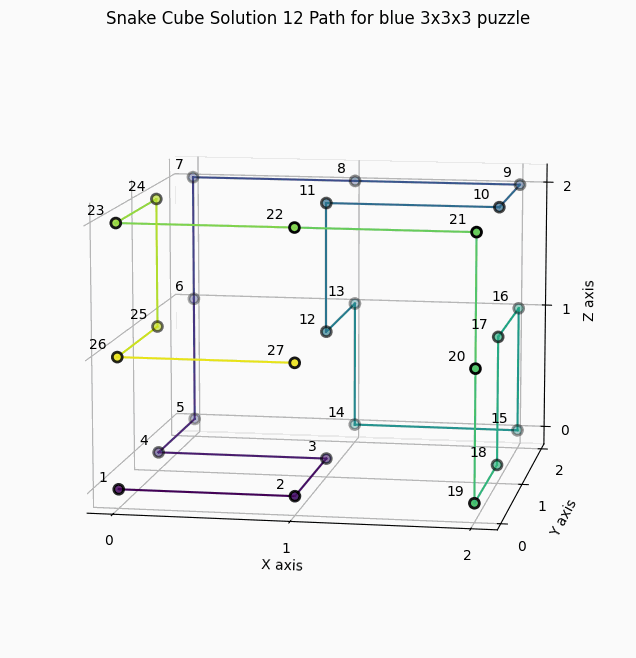
12 Solutions for the blue snake cube with constraints "SCCCCSCSCCCCCCCCCCCSCSCCCCS"

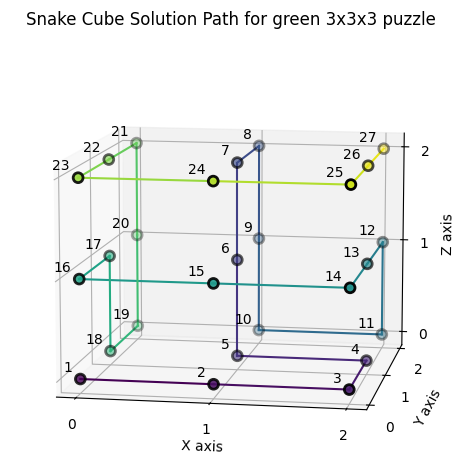
1 Solution for the green snake cube with constraints "SSCCCSCCSCCCSCSCCCCSCSCSCSS"

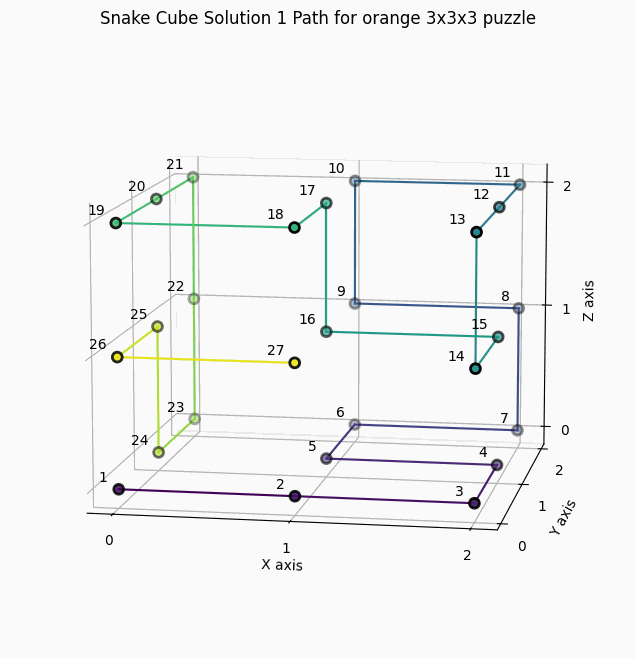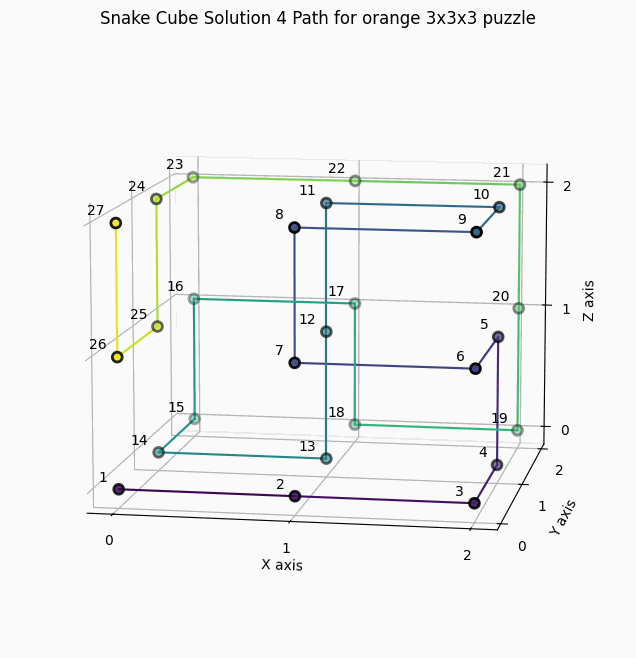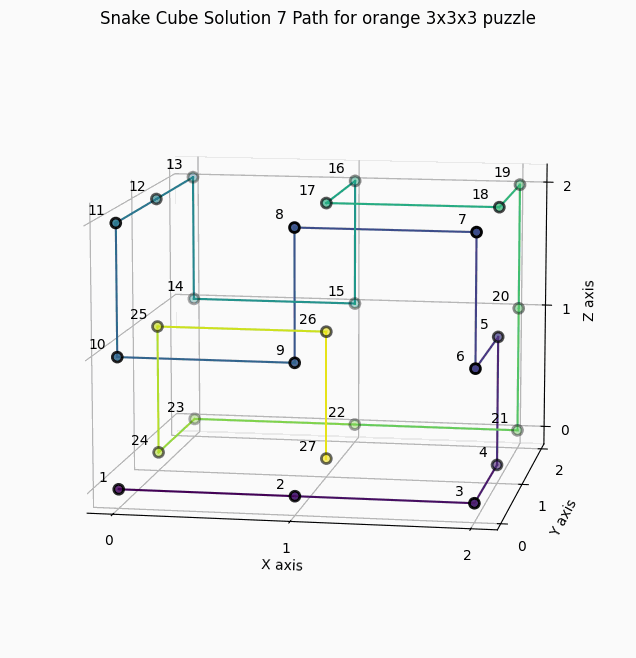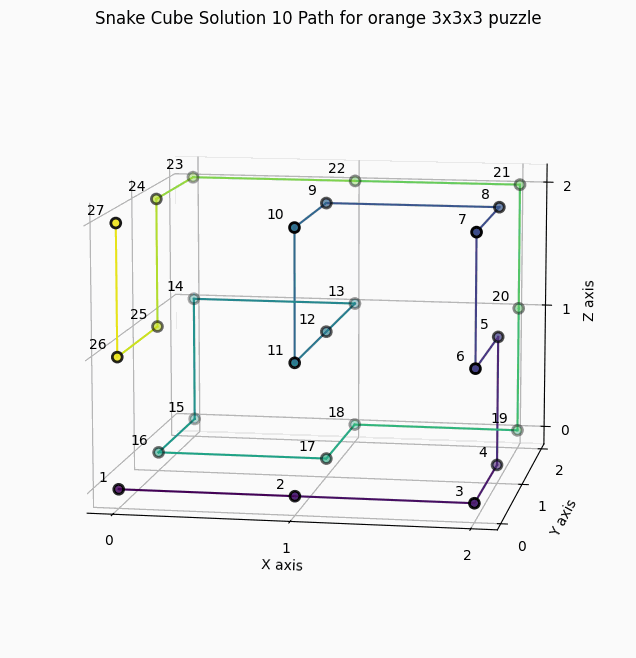
10 Solutions for the orange snake cube with constraints "SSCCCCCCCCCSCCCCCCCSCSCCCCS"

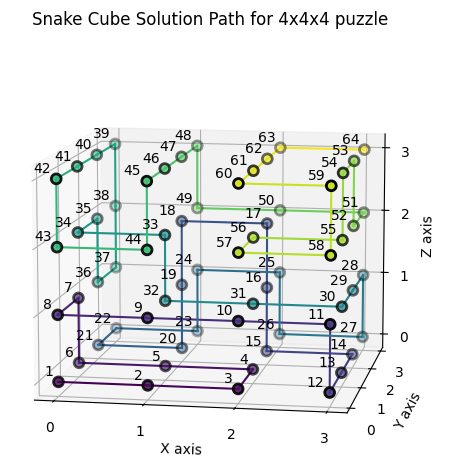
1 Solution for the brown snake cube with constraints:

"CSCCSCCCSSCCSCCSCCSCCCCCCCCCSCSCCCCCCSCSSCCCCSSCCSCCCCCCCCCCSSCC"

Conclusion

The python backtracking script is capable of solving this problem:

• for any of my 3x3x3 cubes in fractions of a second.
• for the given 4x4x4 cube in ~30 seconds.